
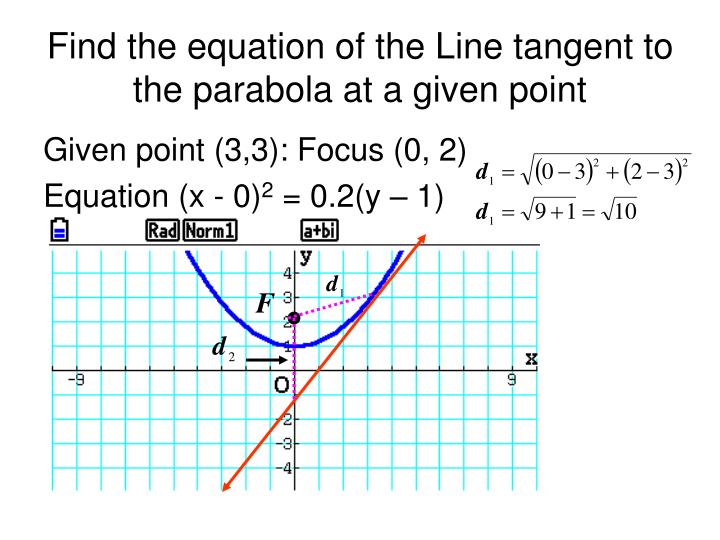
Generally, a hyperbola looks like two oposite facing parabollas, that are symmetrical. Solution: Use the Calculator to Find the Solution of this and other related problems. The eccentricity of an ellipse c/a, is a measure of how close to a circle the ellipseįind the vertices, co-vertices, foci, and domain and range for the following ellipses then graph: (a) 6x^2+49y^2=441 (b) (x+3)^2/4+(y−2)^2/36=1 Techinically, an elipse is defined as a set of points whose distance from two fixed points (called the foci) inside the ellipse is always the same, d1+d2=2a. The line of symmetryįor a horizontal parabola (line of axis is parallel to the x -axis) x=a(y−k)2+h, where (h,k) is the vertex, and y=k is the line of symmetry Note that this can also be written y−k=a(x−h)2 or b(y−k)=(x−h)2+k, where b=1a. A parabola can be represented in the form y=a(x−h)2+k, where (h,k) is the vertex and x=h is the axis of symmetry or line of symmetry Note: this is the representation of an upward facing parabola. Parabolas are commonly occuring conic section. In technical terms, a parabolla is a seto of points that are equidistant from a line (refered to as the directrix) and a point on the line called the focus. Graph of a Circle: Center: (0,0), Radius: 5 Our calculator, helps you find the center and the radius of a circle for any equation. Given any equation of a circle, you can find the center, and radius by completing square method. Geometrically, a circle is defined as a set of points in a plane that are equidistant from a certain point, this distance is commonly refered to as the radius.Ĭenter (0,0): x^2+y^2=r^2Center (h,k): (x−h)2+(y−k)2=r2. General (standard form) Equation of a conic sectionĪx^2+Bxy+Cy^2+Dx+Ey+F=0,where A,B,C,D,E,F are constantsįrom the standard equation, it is easy to determine the conic type egī2−4AC0, if a conic exists, it is a hyperbola More About Circles The calculator generates standard form equations Writing a standard form equation can also help you identify a conic by its equation. This calculator also plots an accurate grapgh of the conic equation The calculator also gives your a tone of other important properties eg radius, diretix, focal length, focus, vertex, major axis, minor axis etcĪnother method of identifying a conic is through grapghing. This conic equation identifier helps you identify conics by their equations eg circle, parabolla, elipse and hyperbola.
#Porabala equation maker given points how to
How to identify a conic section by its equation The conic section calculator, helps you get more information or some of the important parameters from a conic section equation. Among them, the parabola in the most common.

That's why they are commonly refered to as the conic section.Ĭonics includes parabolas, circles, ellipses, and hyperbolas. Conics are a set of curves that can be reproduced by intersecting a plane and a ouble-napped right cone.


 0 kommentar(er)
0 kommentar(er)
